2.6. Résolution et Analyse

2.6.1. Problème de référence

Résumons ici l’utilisation de notre programme éléments finis sur le problème suivant :

(2.8)\[\begin{split}\left\{ \begin{array}{r c l l} -\Delta u + u & = & f & (\Omega)\\ u & = & 0 & (\partial \Omega) \end{array} \right.\end{split}\]

La formulation variationnelle est donnée par

\[\begin{split}\left\{ \begin{array}{l} \text{Trouver }u\in H^1_0(\Omega) \text{ tel que }\\ \displaystyle \forall v \in H^1_0(\Omega), \qquad \int_{\Omega} \nabla u\cdot\nabla v + \int_{\Omega} uv = \int_{\Omega}fv \end{array} \right.\end{split}\]

Pour simplifier nous prenons \(\Omega = ]0,1[\times]0,1[\) le carré unitaire et \(f(x,y) = (1+2\pi^2)\sin(\pi x)\sin(\pi y)\) de sorte que la solution exacte est connue et vaut

\[u(x, y) = g(x, y) = \sin(\pi x)\sin(\pi y).\]

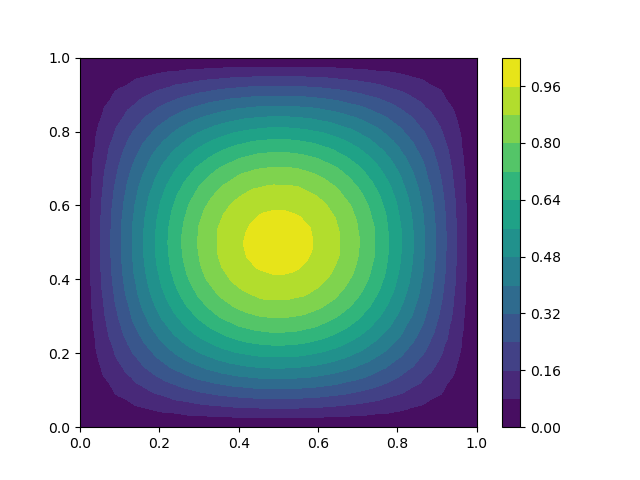
Fig. 2.2 Solution

2.6.2. Résolution

Dans notre programme, cela reviendra à écrire quelque chose comme

#import ...

#Données
def g(x,y):
  return np.sin(np.pi*x)*np.sin(np.pi*y)
def f(x,y):
  return g(x,y)*(2*np.pi*np.pi +1 )
def diri(x,y):
  return 0.
#Maillage
msh = geo.mesher("mesh.msh")
# Triplets
t = common.Triplets()
fem_p1.Mass(msh, 2,10, t)
fem_p1.Stiffness(msh, 2,10, t)
b = np.zeros((msh.Npts,))
fem_p1.Integral(msh, 2, 10, f, b, 2)
fem_p1.Dirichlet(msh, t, b, 1, 1, diri)
# Résolution
A = (sparse.coo_matrix(t.data)).tocsr()
U = sparse.linalg.spsolve(A, b)

# Visualisation
x= [pt.x for pt in msh.points]
y= [pt.y for pt in msh.points]
connectivity=[]
for tri in msh.triangles:
  connectivity.append([ p.id for p in tri.p])

plt.tricontourf(x, y, connectivity, U, 12)
plt.colorbar()
plt.show()

### U de référence
Uref = np.zeros((msh.Npts,))
for pt in msh.points:
  I = int(pt.id)
  Uref[I] = g(pt.x, pt.y)
plt.tricontourf(x, y, connectivity, Uref, 12)
plt.colorbar()
plt.show()

2.6.3. Convergence

Exercise 2.6

1. Pour différents pas de maillage, calculez l’erreur en norme \(L^2\) entre la solution exacte et la solution approchée pour le problème (2.8).

2. Affichez la courbe de l’erreur en fonction de \(h\) en échelle log-log.

3. Calculez la pente de la courbe et déduisez-en la vitesse de convergence par rapport au pas de maillage (\(h\)). Sauvegardez par ailleurs une copie de la courbe en format données (JSON ou autre) ou image (PNG par exemple, pas de JPG nous ne sommes pas des sauvages !).