1. 2017 - 2018 : Wi-Fi#
Ce projet propose d’étudier la propagation des ondes Wi-Fi dans un appartement de \(35\mathrm{m}^2\). Nous ferons appels aux logiciels GMSH, pour la gestion du maillage et la visualisation, et FreeFem++ pour la résolution par éléments finis. Le sujet est décomposé en trois parties : la théorie (le modèle), l’implémentation et l’étude des résultats.
1.1. Équation de Helmholtz#
La définition Wikipédia d’une onde est la suivante :
Une onde est la propagation d’une perturbation produisant sur son passage une variation réversible des propriétés physiques locales du milieu. Elle se déplace avec une vitesse déterminée qui dépend des caractéristiques du milieu de propagation. Une onde transporte de l’énergie sans transporter de matière.
Mathématiquement, une onde \(\mathscr{E}(\xx,t)\) dépend du temps \(t\) et de l’espace \(\xx\), et vérifie l’équation des ondes :
où \(\Delta = \sum_{j=1}^3\frac{\partial^2}{\partial x_j^2}\) est l’opérateur Laplacien (spatiale) et \(c\) est la célérité de l’onde dans le milieu (peut dépendre de \(\xx\) !). Par exemple, dans le cas d’une onde électromagnétique et dans le vide, \(c\) est la célérité de la lumière, soit \(299792458\mathrm{m.s}^{-1}\). La quantité \(\xx\) est un vecteur de dimension \(d=2\) ou \(d=3\) selon le problème considéré : dans notre cas \(d=2\).
Lors d’une excitation périodique, c’est-à-dire lorsque la pulsation \(\omega\) (en \(\mathrm{rad.s}^{-1}\)) de l’onde est fixée, l’onde s’écrit alors \(\mathscr{E}(\xx,t) = \Re\left(u(\xx)e^{-\imath \omega t}\right)\) où \(\imath=\sqrt{-1}\) et \(E\) est une onde spatiale satisfaisant l’équation de Helmholtz :
Cette équation s’obtient en remplaçant \(\mathscr{E}(\xx,t)\) par \(E(\xx)e^{-\imath \omega t}\) dans l’équation des ondes. Nous notons en général \(k = \frac{\omega}{c}\) (en \(\mathrm{rad.m}^{-1}\)) le nombre d’onde et \(\lambda = \frac{2\pi}{k}\) (en \(\mathrm{m}\)) la longueur d’onde, autrement dit, la distance entre deux amplitudes, de sorte que l’équation de Helmholtz s’écrit
Les ondes Wi-Fi qui suivent la norme IEEE 802.11g sont émises à une fréquence variant de \(2.4\mathrm{GHz}\) à \(2.5\mathrm{GHz}\). Dans notre projet, nous nous limiterons à des ondes de fréquence \(2.4\mathrm{GHz}\) textbf{si votre machine vous le permet !} En effet, les simulations de propagation d’ondes sont parmis les plus coûteuses en terme de CPU. Si votre machine n’est pas assez puissante, nous prendrons une onde de fréquence plus faible, comme \(1\mathrm{GHz}\) voire moins.
Exercise 1.3
Sachant que \(\omega=2\pi F\) où \(F\) est la fréquence, en Hertz (\(\mathrm{Hz}\)), calculez le nombre d’onde \(k\) et la longueur d’onde \(\lambda\) dans le vide, pour une onde électromagnétique et pour \(F=2.4\mathrm{GHz}\) et \(F=1\mathrm{GHz}\).
1.2. Modèle#
1.2.1. Entre les murs#
Nous notons \(\Omega\) l’appartement tout entier dans lequel est situé notre routeur. Les murs sont supposés être du même matériau : du placo-plâtre. Le domaine \(\Omega\) est décomposé en deux domaines :
où \(\Omega_{\text{air}}\) est l’intérieur de l’appartement, composé d’air (nous le supposerons vide de meubles), et \(\Omega_{\text{mur}}\) contient les murs en placo-plâtre. Nous ne prendrons pas en compte les appartements voisins au nôtre. De plus, nous nous limiterons à la dimension \(2\) de l’espace.
L’air est modélisé comme étant le vide : \(c_{\mathrm{air}} = c\), tandis que, pour les murs en placo-plâtre, nous avons \(c_{\mathrm{placo}} = \frac{c}{2.4}\). Plutôt que de rendre le nombre d’onde dépendant de l’espace, nous introduisons la fonction de contraste \(n\) définie par:
Nous modifions alors l’équation de Helholtz ainsi :
Le nombre d’onde \(k\) est donc ici celui de l’air (ou du vide).
1.2.2. Le routeur : la fonction \(f\)#
Idéalement, le routeur devrait être modélisé comme un point source et donc mathématiquement par la distribution de Dirac \(\delta_{\mathbf{x}_s}\) centré sur la position \(\mathbf{x}_s\) du routeur. L’équation à résoudre serait alors :
Cependant nous ne pouvons pas utiliser de distribution de Dirac avec la méthode des éléments finis (car \(\delta_{\mathbf{x}_s}\not\in L^2(\Omega)\)). Nous modélisons alors le routeur par un disque \(\Omega_{s}\) de rayon \(\varepsilon_s = 0.1\) et de centre \(\mathbf{x}_s = (x_s,y_s)\) et la distribution \(\delta_{\mathbf{x}_s}\) est approchée par la fonction chapeau \(f_s\) définie par
La fonction \(f_s\) est d’intégrale totale égale à \(1\) et quand \(\varepsilon_s\) tend vers \(0\), la suite de fonction \((f_s)_{\varepsilon_s}\) tend vers la distribution de Dirac \(\delta_{\mathbf{x}_s}\).
Exercise 1.4
Montrez que :
Pour simplifier, on pourra se placer dans le cas où \(\Omega_{s}\) est centré en \((0,0)\) et utiliser un changement de coordonnées adéquat.
1.2.3. Réflexions parasites#
Sur le bord extérieur de notre appartement, nous souhaitons que l’onde ne se réfléchisse pas, pour cela nous imposons la condition aux limites suivantes:
Cette condition est une approximation de la condition non réfléchissante exacte : l’onde sera légèrement réfléchie, toutefois la mise en oe{}uvre d’une telle condition reste très simple et peu coûteuse, ce qui explique que nous l’utilisions. Notez que \(\nn\) est le vecteur normale unitaire sortant à \(\Omega\) (ne pas confondre avec \(n\) la fonction de constraste).
1.2.4. Le système à résoudre#
Au final, le système que nous devons résoudre est le suivant. Nous cherchons l’onde spatiale textbf{complexe} \(E\), telle que, pour \(k = \omega/c\) donné, elle vérifie :
1.2.5. Formulation variationnelle#
Exercise 1.5
Montrez que la formulation variationnelle du problème (ref{eq:helmholtz}) s’écrit
avec
Exercise 1.6
Montrez que les applications \(a(\cdot,\cdot)\) et \(\ell(\cdot)\) sont continues sur respectivement \(\Ho\times\Ho\) et \(\Ho\).
Malheureusement pour nous, \(a(\cdot,\cdot)\) n’est pas coercive : nous ne pouvons pas appliquer le Théorème de Lax-Milgram et de ses corollaires. Nous admettrons le Théorème suivant
1.3. Implémentation#
1.3.1. Le pas de maillage#
Pour résoudre des problèmes de propagation d’ondes, le pas de maillage (ou la finesse de maillage), noté \(h\) (diamètre du plus grand élément), dépend du nombre d’onde \(k\), ou plutôt, de la longueur d’onde \(\lambda = 2\pi/k\). En effet, si nous ne prenons pas assez de points de discrétisation, l’onde ne sera pas suffisamment approchée comme le montre la Figure 1.2. Cela rejoint le Théorème de Shanon d’échantillonage.
En pratique, nous prenons un nombre de points \(10 \leq n_{\lambda} \leq 20\) par longueur d’onde. Autrement dit, nous avons, si \(h\) est la taille caractéristique d’un élement :
Il faudra veiller, lors de nos simulations, à ce que \(n_{\lambda} = 10\) textbf{au minimum}. Pour les simulations finales à haute fréquence, il vaut mieux privilégier \(n_{\lambda} = 15\) ou \(n_{\lambda}=20\), si la machine le permet.
Remark 1.2
Avant de lancer un calcul et/ou un maillage pour tester (i.e mon code plante-il ?) : choisissez un nombre d’onde faible ! Par exemple \(k= 10\) ou \(k=5\) (mais pas \(k=0\) !).
Fig. 1.2 Illustration d’un échantillonage trop faible en 1D : la solution discrète est linéaire et non oscillante ! Elle est trop éloignée de la solution exacte. Nous avons besoin de plus de points de discrétisations.#
1.3.2. L’appartement : GMSH#
Fig. 1.3 Plan de l’appartement (en mètre). Rappelons que \(\Omega = \Omega_{\text{air}}\cup\Omega_{\text{mur}}\) et \(\partial\Omega\) est le bord « externe » de l’appartement.#
Le plan de l’appartement que nous considérons est donné par la Figure 1.3 où chaque dimension est exprimée en mètre. Nous proposons les contraintes suivantes sur l’appartement : sa longueur \(L\) est fixée à 7, sa largeur \(\ell\) à 5 et l’épaisseur \(d\) des murs est égale à 0.2.
Exercise 1.7
Implémentez un code GMSH qui reproduit le plan de la figure 1.3, en respectant las consignes suivantes :
Nous devons être en mesure de pouvoir modifier via l’interface graphique les quantités suivantes :
Le nombre de points \(n_{\lambda}\) de discrétisation par longueur d’onde \(\lambda\). N’oubliez pas que \(n_{\lambda}\) est un entier.
La position du routeur \(\mathbf{x}_s\) (Il n’est pas nécessaire de contraindre/vérifier sa position par rapport aux murs (mais par rapport aux dimensions de l’appartement, oui !), nous supposerons l’utilisateur suffisamment malin pour cela)
Remarque : dans la version originale du projet, il était demandé de pouvoir modifier les dimensions des pièces et donc de pouvoir déplacer les murs.
La largeur des portes est fixées à \(80\mathrm{cm}\).
Le rayon de \(\Omega_{s}\) est fixé à \(0.1\mathrm{cm}\).
Tous les murs sont de même épaisseur \(d\).
Remark 1.3
À vous de définir les entités Physical qui vous semblent d’importance ainsi que les dimensions des pièces.
1.3.3. La formulation variationnelle : FreeFem++#
Exercise 1.8
Rédigez le code freefem permettant de résoudre le problème (1.2) dans le maillage réalisé par gmsh. Les quantités en sorties qui nous intéressent sont :
Le champ \(u\) : partie réelle et partie imaginaire, dans tout l’appartement.
La valeur absolue du champ : \(\abs{u}\), dans tout l’appartement.
Remark 1.4
Plusieurs remarques :
Vous pouvez rédiger un script qui modifie le nombre d’onde \(k\) dans le(s) fichier(s) freefem et gmsh, puis lance gmsh et freefem… En bref : vous êtes libre de geeker comme bon vous semble.
En phase de test, rappelez-vous de textbf{ne pas lancer} de résolution du problème pour un \(k\) élevé.
Mettez la solution à l’échelle : faites en sorte que le maximum de la solution soit égale à \(1\).
La solution que l’on calcule présente très certainement un pic au niveau du routeur, qui empêche de visionner correctement la solution en dehors de celui-ci. Il peut, dès lors, être intéressant de regarder la solution obtenue partout en dehors du routeur et/ou de modifier la range de couleur.
1.4. Étude et examen oral#
Maintenant que nous disposons d’un code qui permet de résoudre le problème de propagation d’ondes Wi-Fi dans un appartement, nous pouvons le tester.
Il n’y a ici plus d’exercice à proprement parler : à vous d’effectuer les simulations qui vous paraissent intéressantes et de sauvegarder les résultats issus de ces résolutions en vue de les présenter à l’oral. La qualité des réponses et le nombre de questions traitées seront pris en compte. Soyez rigoureux/rigoureuses et précis(es) : notez scrupuleusement les paramètres utilisés, ne vous embrouillez pas entre les différentes simulations, sauvegardez les fichiers images et les fichiers de données, …
Nous donnons ici quelques idées de questions à se poser :
Si le routeur est situé obligatoirement dans le salon et le long du mur « gauche », peut-on lui trouver une place pour pouvoir toujours être connecté au Wi-Fi tout en étant aux toilettes ? (nous pouvons par exemple supposer qu’en deça de \(25\%\) de la puissance max, la réception n’est pas suffisante pour glander sur youtube).
À défaut de trouver l’optimal, quel serait un bon emplacement pour le routeur, pour obtenir du réseau Wi-Fi partout ?
Sachant que l’indice \(n\) du béton est de l’ordre de \(7\). Que se passe-t-il si un des murs de l’appartement est en béton (mur porteur) ? Pouvons-nous obtenir une cartographie des différences entre la solution avec mur en placo et avec un mur porteur ?
Influence du pas de maillage sur la solution ?
Que se passe-t-il si les murs deviennent comme de l’air (\(n(\Omega_{\text{mur}})=1)\)) ? Pouvons nous obtenir une cartographie des différences entre la solution avec mur en placo et mur « en air » ?
Et si les murs étaient en béton (\(n=7\)) ?
Et si c’était votre appartement ?
…
Réfléchissez également à d’autres questions plus théoriques et essayez d’apporter des réponses, comme par exemple
Quelle sont les limites du modèle ?
Que et comment pourrions nous améliorer notre modèle et notre code si nous disposions d’une machine de puissance infinie ?
Quelles améliorations, du point de vue géométrique, pouvons-nous apporter à notre appartement ?
Plus que l’obtention de réponse « parfaite », ce sera votre capacité et votre volonté de recherche qui seront pris en compte.
1.5. Résultat#
1.5.1. Exemple#
La figure 1.4 illustre un exemple de ce que l’on peut obtenir.
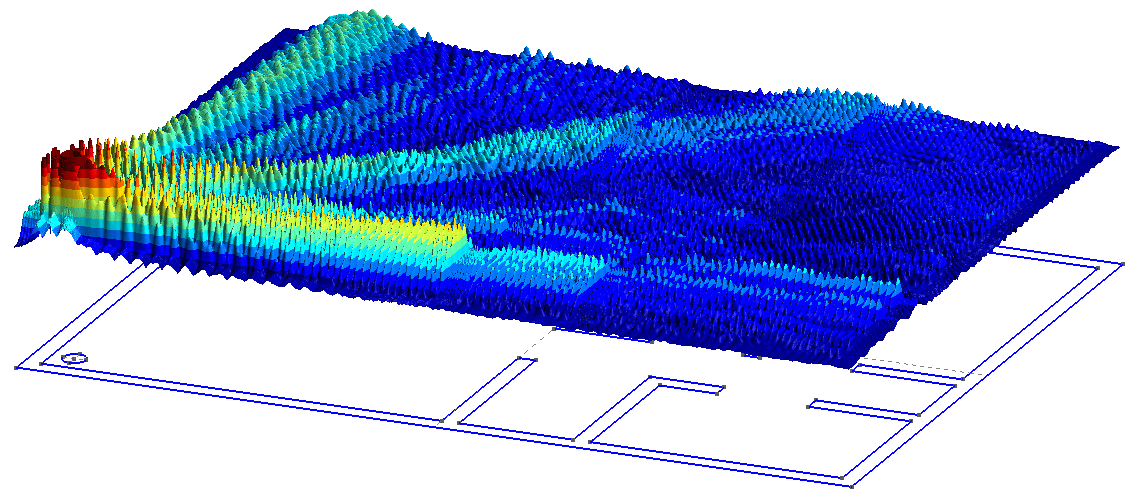
Fig. 1.4 Propagation d’une onde Wi-Fi dans un appartement. Après avoir traversé 2 murs, l’onde Wi-Fi semble très amortie. Sous le résultat est affiché le plan de l’appartement et la position du routeur (petit disque à gauche)#
1.5.2. Vous voulez tester ?#
Téléchargez le bundle Onelab. Il contient GMSH et GetDP (un solveur éléments finis)
Téléchargez le code, soit directement soit via Git :
git clone https://github.com/Bertbk/wifi.git wifi
Dans le dossier et dans un terminal, lancer
gmsh wifi.proVous pouvez modifier un peu la géométrie et la fréquence de l’onde, mise à 1GHZ. Attention, cette simulation est très gourmande : testez d’aborg avec 1GHz avant de lancer la simulation pour 2.5GHz (au risque de faire crasher votre ordinateur) !